平面図形の問題の解説を読んでいると、急に「~に補助線を引く」とか出てくることがあります。そして、その補助線を使うとうまいこと問題が解けますよー、みたいな。
でも解説読んでる側からすると、「どうしてそこに補助線引くの?」「そんな天才みたいな発想思いつかないよ」となることがほとんどですよね。
でも、補助線引くパターンって整理すれば実はかなり限られているんです。今回はそんな「どういうモチベーションで補助線を引くのか?」「実際どのように補助線を引くのか?」ということを紹介しようと思います。
ポイントはこちらです。
知っている形を作るために補助線を引け!!
補助線を引く目的は…
これはずばり「知っている形をつくること」だと言えます。
平面図形の一番最初の記事で、平面図形の問題では「形に反応することが大事だ」と教えました。しかし、必ずしも全ての問題で知っている形がそのまま出てくるとは限りません。知っている形のうち一部分が欠けていたり、線が足りなかったりすることもあります。
ただ逆に言えばそんな形は「あとちょっと線があれば知っている形になる」わけですよね。補助線はそんなときに引くものなのです。
例えば、蝶々型を紹介した記事ではこんな図がでてきましたね。
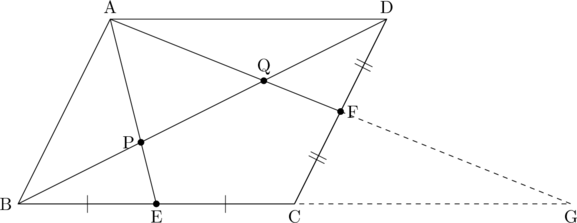
破線のように補助線を引くことで、蝶々型という知っている形が出てきています。
知っている形さえ作れれば、そこからどんな情報が得られるかというのはもう普段の勉強の中で学んでいるわけですから、ここから先は普段通りやれば良くなるわけですね。
逆に、知っている形も作れないのにいたずらに補助線を引くのは全くの無意味であるということです。そういうことをしないように、これはポイントにしておきましょう。
知っている形を作るために補助線を引け!!
補助線の引き方3選
知っている形を作れるからといって、どんなふうに線を引いても良いというわけではありません。それを許すと、何も無いところにさえ知っている形を書き足すことができてしまいます。それだとあまりにも方針としてゆるゆる過ぎるので、ここでは基本的な補助線の引き方というものを教えましょう。
既にある線を延長する
これが一番よくやるやり方だと思います。先ほどの例でも、

平行四辺形ABCDの辺BCと、線分AFを延長することで蝶々型を作っていました。
中心的なところから線を引く
これがおそらく2番目によくやる方法です。円の中心から線を延ばして半径を作るとか、皆さんよくやりますよね。それのことです。
円の中心はもちろん中心ですが、正多角形にも中心がありますね。そこから頂点に向けて線を引くというのも結構あります。例えば正六角形の中心から下図のように線を引いてみると…
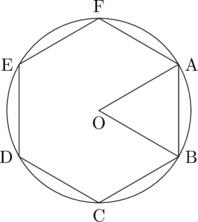
正三角形OABという見慣れた形が出てきますね。
既にある線と平行な線を引く
これは、もし出題されたら割と難しい部類に入ると思いますが…でも、平行線というのはかなり情報の多い図形ですから、使いこなせれば非常に強い武器になるでしょう。
この補助線の引き方の典型例としては、外角の二等分線公式の証明が挙げられます。
下図において、AB:AC=BD:DCが成り立つ。
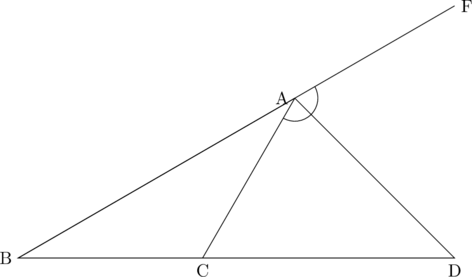
この証明は、以下のようになります。
点Cを通りADと平行な線を引き、それとABの交点をEとします。
すると以下のように角共有型の相似(△BCE∽△BDA)が見えますね。知っている形が出てきたので嬉しいわけです。
さらにこのときAD,ECが平行線であることを利用すると、印をつけたところの角は全て等しいですから、特に△AECは二等辺三角形であるとわかります。それゆえAC=AEです。
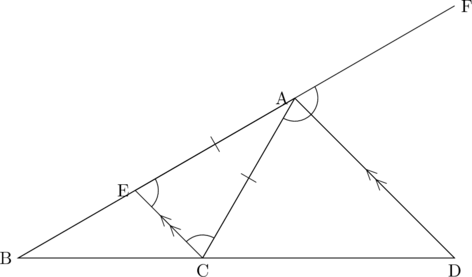
したがって、相似よりAB:AE=BD:DCであることと合わせると、AB:AC=BD:DCであることが分かります。
このように、定理の証明などから学べることも多いので、意欲のある人は他の定理の証明なども読んでみることをおすすめします。
今回の宿題
- 中学2年の単元「空間図形」などから、問題15問以上
を、今回の説明を意識して解いてみてください。
学校で配られた問題集でも、ネット上の問題でも大丈夫です。


