2020年度(令和2年)都立青山高校の入試で出題された数学の解説をします。今回は大問3,4の解説です。
大問1,2はこちら。
大問3の問1は割とやさしめで、合格のためには取りたい問題でした。しかし問2は難しく、本番では下手に時間を無駄にしないよう捨てるという判断も必要だったかもしれません。
大問4は丁寧かつ確実に計算をこなしていけば、安定して得点できる問題でした。ただし問2などは、まず条件が成立するような場合は何秒後なのか?を求めなければいけないことに気づけなかった人もいるかもしれませんね。普段から、答えを求めるために必要なものを順番にきちんと考える、という練習をしておきましょう。
大問3
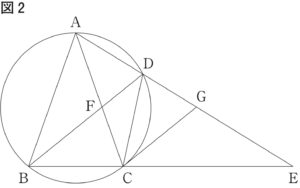
下の図 1 で四角形 ABCD の 4 つの頂点は,すべて同じ円の周上にあり,AB=ACである。線分 AD を D の方向へ延ばした直線と線分 BC を C の方向へ延ばした直線の交点を E,線分 AC と線分 BD の交点を F,点 C を通り線分 BD に平行な直線と線分 AE との交点を G とする。次の各問に答えよ。

〔問 1 〕
(1) 図 1 において,∠BAC=a°,∠CAE=b°とするとき,∠BEA の大きさは何度か。a,b を用いて表せ。
(2) 図 1 の中に △ACD と相似な三角形がいくつかある。その中から 1 つを選び,選んだ三角形を解答欄に示せ。また,選んだ三角形が △ACD と相似であることを証明せよ。
〔問 2 〕図 2 は図 1 において BC=CD の場合を表している。AB=9 cm,BC=6 cm のとき,線分 GEの長さは何 cm か。
問1
(1)
∠BEAの大きさを出すために使える道具は何か?を考えます。すると、今回与えられている角が∠BACと∠CAEなので、△BEAの内角の和を利用できるかも?と気づきますね。
内角の和から∠BEAの大きさを出すためには、∠BAEと∠ABEの大きさが必要ですから、これをaとbを使って表しましょう。
- ∠BAE=∠BAC+∠CAE=(a+b)°
- △ABCが二等辺三角形で、∠ABEがその底角であることより、∠ABE=\frac{180-a}{2}°
です。よって、
∠BEA=180°-∠BAC-∠ABE=(90-\frac{1}{2}a-b)°
が答えとなります。
(2)
△ACDと相似な三角形をまず探せ…ということなのですが、一番見つけやすいのは△ACD∽△AECという反転型の相似でしょう。今回は図がかなり正確に書かれているので(都立高校の問題では正確な図が載っていることが多いですね)、図を見て直感的に分かった人も多いと思います。
∠CADは共通ですから、もう1組等しい角を見つければ相似の証明ができますね。今回は(1)で∠BEAをaとbを使って表しましたから、(1)が誘導だったのだということに気づいて、∠BEA=∠ACDを示そうと考えられます。つまり、∠ACD=(90-\frac{1}{2}a-b)°を示せば良いわけですね。
ただし、これを示すのは決して難しくありません。a,bで示されている角と∠ACDの位置関係を見れば、円に内接する四角形の対角の和が180°であることを利用することに気づくはずです。さらにそこで余分となる∠BCAは、(1)で既に∠BCA=∠ABE=\frac{180-a}{2}°として求められています。したがって、
∠ACD=180°-(∠BAC+∠CAD)-∠BCA=(90-\frac{1}{2}a-b)°
となり、証明することができます。
問2
問1で相似に注目させられているわけですから、それが問2への誘導になっていると考えるのが自然でしょう。つまり「相似を利用して問2を解いてね」ってことです。
問1(2)で示した相似は△ACD∽△AECでしたが、問題文には「相似な三角形がいくつかある」と書いてあるので、相似な図形の組はこれだけではないはずですね。というわけで△ACDと相似な図形を探していくと…
- △AEC
- △BED(円周角の定理を使うと△AECと相似だと分かるから)
- △CEG(BD//CGを使うと、角共有型で△BEDと相似だから)
が見つかります。さて、今回求めたいものはGEの長さでしたね。よって、GEをドンピシャで含んでいる△CEGと△ACDの相似を利用すれば良いのでは?と思いつきます。そして実際、
- ACとCEが対応していて、AC=9cm
- DCとGEが対応していて、DC=6cm
ですから、CEの長ささえ分かれば相似比が分かって、そこからGEの長さが分かりそうです。というわけで当面の目標は、CEの長さを出すことになります。
ところが、CEの長さは簡単には出ません。方べきの定理や相似を使おうにも、なかなかうまく当てはまらないのです。
そこで、行き詰まったら条件に立ち返りましょう。今回二等辺三角形BCDという条件がありました。二等辺三角形といえば底角に注目するのがよくあるパターンですから、底角と等しいところに印を付けていくと…
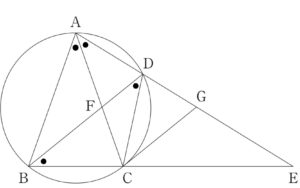
このように、∠BAC=∠CAEであることに気づきます。つまり、ACは∠BAEの二等分線であるということです。そこで、こんな定理を紹介しましょう。
下図において、ADが∠BACの二等分線であるとき、
AD^2=AB\times AC-BD\times DC
が成り立つ。
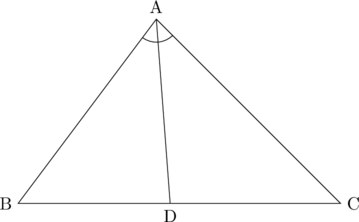
これを用いることで、角の二等分線の長さを利用することができます。今回で言うとAC=9cmのことですね。
というわけで、この公式にそれぞれの長さを当てはめていきます。cmを省略し、CE=xとおくと、
- AB=9
- BC=6
- CE=x
- AE=\frac{3}{2}x(△ACD∽△AECを利用)
となります。よって公式より、
9^2=9\times \frac{3}{2}x-6x\\
\therefore x=\frac{54}{5}です。したがって△CEGと△ACDの相似比が6:5と分かるので、EG=\frac{36}{5}ということが分かるのです。
ちなみに今回の問題は、角の大きさを図に書き込んでいくと
- △ABC≡△ACG
- △ABC∽△CDG
であることが分かります。よってAG=9cm、CD=6cm、DG=4cm、AD=5cm…などの情報が分かり、△ACD∽△CEGの相似から答えが出ます。
ただしこれに気づくのはひらめかないときびしいなぁということ、および角の二等分線の長さ定理を紹介したかったので、解説では上記のように解いています。
大問4
下の図 1 は 1 辺の長さが 12 cm の正四面体 ABCD の展開図である。この展開図を組み立てた正四面体 ABCDにおいて,点 P は頂点 A を出発して毎秒 1 cm の速さで辺 AD 上を頂点 D に向かって移動し,頂点 D に到着して止まる。点 Q は点 P が頂点 A を出発してから 2 秒後に頂点 A を出発して毎秒 \frac{3}{2} cm の速さで辺 AC 上を頂点 Cに向かって移動し,頂点 C に到着して止まる。次の各問に答えよ。
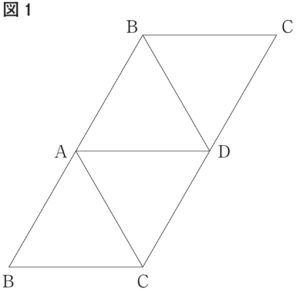
〔問 1 〕点 P が頂点 A を出発して 2 秒後の線分 PB の長さは何 cm か。
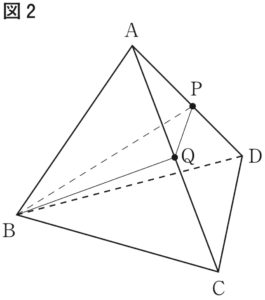
〔問 2 〕下の図 2 で示した立体は,図 1 を組み立ててできた正四面体であり,頂点 B と点 P,点 P と点 Q,点 Q と頂点 B をそれぞれ結んだ場合を表している。PQ//DC となるとき,△BQP の面積は何 cm^2 か。
〔問 3 〕 図 1 を組み立ててできた正四面体 ABCD の体積を V_1 cm^3,点 P が頂点 A を出発して8 秒後の四面体 ABQP の体積を V_2 cm^3 とする。V_1:V_2 を最も簡単な整数の比で表せ。ただし,答えだけでなく,答えを求める過程が分かるように,途中の式や計算なども書け。
問1
2秒後の点Pの様子を△ABD上で書き出してみれば、三平方の定理より答えはすぐに出ます。
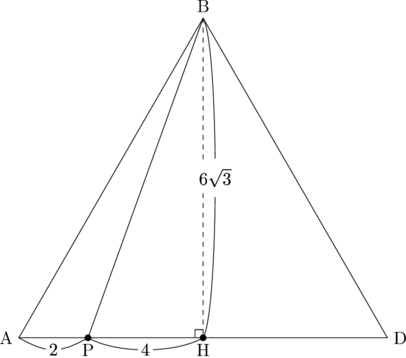
点Bから辺ADに下ろして垂線の足を点Hとしています。
ここで△PBDに三平方の定理を使えば、PB=\sqrt{4^2+(6\sqrt{3})^2}=2\sqrt{31}と分かります。
問2
まず考えなければいけないのは、PQ//DCとなるのは何秒後のことか?ということですね。そもそもこれが分からなければ、点Pや点Qがどこにあるのかという、図形のハッキリとした形が定まりません。
点Pの出発からt秒後にPQ//DCになるとしましょう。このときAP=t, AQ=\frac{3}{2}(t-2)と表せます。PQ//DCならばAP=AQのはずですから、これを使ってtを求めると、
t=\frac{3}{2}(t-2)
t=6
となります。つまり点Pの出発から6秒後、AP=AQ=6となる場所に点P,Qがあるということですね。
図形がどんな形をしているかが分かったので、あとは計算で△BPQの面積を求めていきます。正四面体ABCDは対称性の良い形をしているので、△BPQがBP=BQの二等辺三角形であることは良いでしょう。よって△BPQは
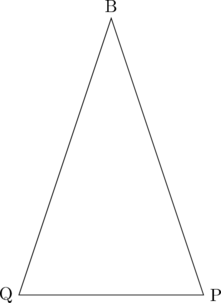
こんな形をしているはずです。△BPQの面積を知るには高さと底辺の長さが必要なので、1つずつ考えていきます。
底辺の長さは、△APQ∽△ADCという角共有型の相似を利用すればすぐに分かります。相似比がAP:ADより1:2ですから、底辺の長さPQ=6です。
高さを求めるには、この例題のように三平方の定理を使うのが定石です。そのために△BPQに点Bから垂線を引くと、△BPQは二等辺三角形であり、
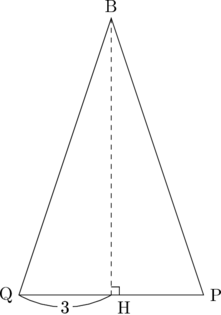
垂線の足Hは底辺PQを二等分するので、QH=3であると分かります。したがってBQの長さが分かれば高さも求められますね。BQは△ABC上にあるので、△ABC上がどんな形になっているか図に描いてみると、

点QはACの中点なので、正三角形ABCにおいて点BからACに下ろした垂線の足と一致しています。よってこの図より、BQ=6\sqrt{3}です。したがって高さBHを三平方の定理から求めるとBH=3\sqrt{11}となり、△BPQは
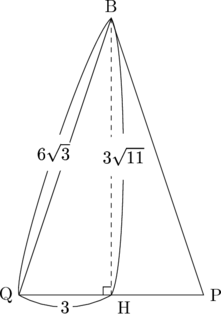
となります。したがって面積は、
△BPQ=\frac{1}{2}\times 6\times 3\sqrt{11}=9\sqrt{11}
であると得られます。大事なことは、一つ一つ丁寧に平面図を書いていくことですね。
問3
三角形ACDの面を底面と見ると、V_1もV_2も高さが同じ三角錐であることが分かります。
面積比のポイントを応用して、体積比を求める時も共通している部分以外に注目すれば十分であることに気づきましょう。つまり、V_1とV_2の体積比は、それぞれの底面積の比に等しいということです。
したがって、△ADCと△APQの面積比を求めていきます。点Pが点Aを出発してから8秒後の話をしているので、△ADCはこんな状況になっています。
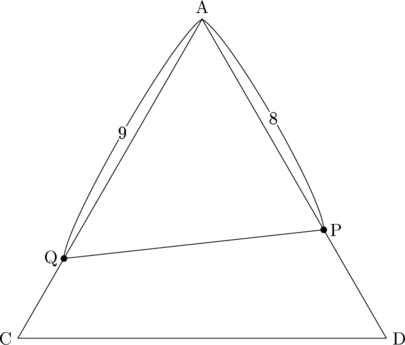
△ADCと△APQの面積比は一角共有の面積比ですから、ここまで整理できれば面積比は簡単に求まります。
△ADC:△APQ=12×12:8×9=2:1
よって、V_1:V_2=△ADC:△APQ=2:1となります。


コメント