【過去問】2021(令和3)年都立新宿高校数学【前編(大問1,2)】

この記事に掲載されている過去問の問題文や図は、高校の公式HPからの引用です。
元の問題を見たい人は以下のボタンから問題・解答に飛ぶことができます。

2021年度（令和3年）都立新宿高校の入試で出題された数学の解説をします。今回は大問1，2の解説です。
大問3，4はこちら。

大問1は基本的に頻出問題でした。問題集で学んできた解法を適切に使えるかどうか？というのが問われたと思います。

大問2の問1、問2(2)は難しくありませんでしたね。問2(2)は誘導もしっかりついていて迷うところがなかったでしょう。ただし問2(1)は難しい部類だったと思います。適切に考察できるかというのが問われ、中途半端なところまでしか考察できないと鬼のような計算をするはめになります。大問の真ん中にこういう問題があると、「位置的に解けるはずなのに解けない…！」と本番焦ってしまう受験生も多いでしょう。難しいものは難しいと冷静に判断するのも大切ですね。

今回初出のポイントはこちらです。

桁を入れ替える問題では、各桁を文字でおけ！
内側に回転軸のある回転体は、対称に書き直してから回転させろ！

大問1
1. 問4
2. 問5
大問2
1. 問1
2. 問2
  1. （1）
  2. （2）

大問1

問1，2，3, 6は簡単なので省略します。

問4

問題文

Aは4桁の自然数とする。Aの千の位の数と一の位の数を入れ替えた数をBとすると，Bは5の倍数である。Aの十の位の数と一の位の数を入れ替えた数をCとすると，Cは10の倍数である。Aの千の位の数と百の位の数を入れ替えた数をDとすると，D-A=3600である。Aが3の倍数で，ーの位の数が素数であるとき，Aを求めよ。

桁を入れ替える系の問題です。このパターンでまずやることは1つですね。

桁を入れ替える問題では、各桁を文字でおけ！

これ以上でもこれ以下でもありません。というわけでAの各桁を大きい順にa, b, c, dとして、A=1000a+100b+10c+dとします。

Bは5の倍数です。5の倍数は一の位が0か5ですから、a=0 or 5です。ただしa=0だとAが4桁の数ではなくなってしまうので、a=5しかありえないことが分かります。

Cは10の倍数です。10の倍数は一の位が0ですから、ｃ＝0だと分かりますね。

ここまでで、Aは5b0dという形をしていることが分かりました。よってDはb50dとなりますから、Dの方が3600大きいことよりｂ＝9であると分かります。

よってAは590dという形をしています。条件ではAが3の倍数であると言っていますね。3の倍数は各桁を足した和が3の倍数になるので、5+9+0+d=14+dが3の倍数になります。さらにdは素数であるという条件が最後の最後にありますから、ｄ＝7です。

したがってA=5907が答えです。各桁さえ文字で置けばあとは問題文の順番通りに条件を当てはめていくだけですが、その条件の使い方（3の倍数なら各桁の和が3の倍数など）が分からないと厳しいものがあったでしょう。

問5

問題文

下の図1で，四角形ABCDは，AD//BC,AD = 3 cm, BC = 6 cmの台形である。頂点Aと頂点Cを結ぶ。AC= 4 cm, ∠ACB=∠CAD=90゜となるとき，この四角形ABCDを線分ACを軸として1回転したときにできる立体の体積は何 $cm^3$ か。ただし，円周率は $\pi$ とする。

回転する図形の内側に回転軸があるときは、回転によって重なる部分を考慮しなければいけません。
ただし頭の中で「ここがこれだけ回転するから、ここが重なって…」など考えるのは大変ですし、ミスも増えます。よって以下の手順で、何が回転するのかを書き直すことをおすすめします。

回転軸に対して左側の部分を右側に、右側の部分を左側に対称に移す。
回転軸より左側（右側でも良い）の部分を削り取る。

今回の図形で言うと、上の1．の手順によって

Rendered by QuickLaTeX.com

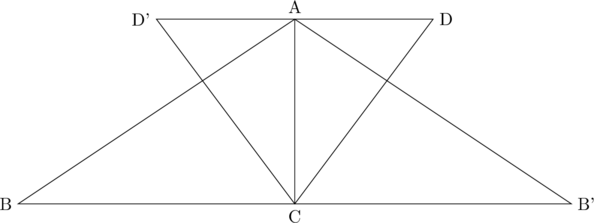
のようになり、2．の手順で、

Rendered by QuickLaTeX.com

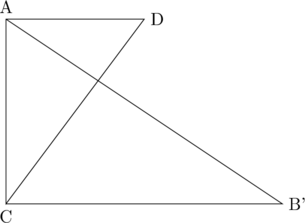
となります。こちらの図形をAC軸に回転させることと、元の図形を回転させることは全く同じことです。こちら側で色々考えた方が情報が得やすいので、内側に軸がある回転体は図を書き直すようにしましょう。

内側に回転軸のある回転体は、対称に書き直してから回転させろ！

では書き直したこの図形を回転させた体積をどう求めるか？ですが、これは線分AB’とCDの交点をEとして、

(△AB’Cの回転体)＋(△ACDの回転体) – (△ACEの回転体)

として求められますね。このように一旦重複して求めてからオーバーした分を引くというやり方はいろいろなところで出てくる（ベン図など）ので覚えておくと良いでしょう。

EからACに下ろした垂線の足をHとすれば、蝶々型の相似（△ADE∽△B’CE）よりAE:EB’＝1:2で、これと角共有型の相似（△ACB’∽△AHE）よりEH＝2と分かります。これで△ACEの回転体の体積を出すこともできますね。

従って答えは

\begin{aligned} \frac{1}{3}\times4\times \pi \times6^2+\frac{1}{3}\times4\times \pi \times3^2-\frac{1}{3}\times4\times \pi \times2^2=\frac{164}{3}\pi \end{aligned}

となります。

大問2

問題文

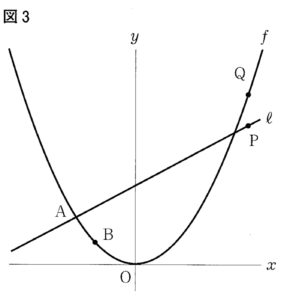
下の図1で，点0は原点．曲線fは関数 $y=\frac{1}{4}x^2$ のグラフ，直線 $l$ は関数 $y=\frac{1}{2}x+\frac{15}{4}$ のグラフを表している。曲線fと直線 $l$ との2つの交点のx座標は，それぞれ-3と5であり，x座標が-3の点をAとする。直線 $l$ 上にある点をP, 曲線f上にある点をQとし，2点P,Qのx座標はともに-3より大きい数とする。原点から点(1,0)までの距離および原点から点(0,1)までの距離をそれぞれ1cmとして，次の各問に答えよ。

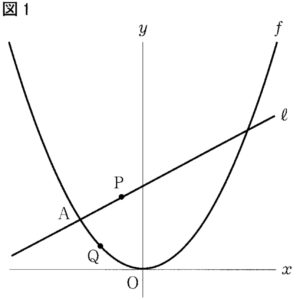
〔問1〕点Aと点Q,点Pと点Qをそれぞれ結び，2点P,Qのx座標をともに-1とした場合を考える。△APQの面積は何 $cm^2$ か。

〔問2〕下の図2は，図1において，曲線f上にあり，X座標が-2である点をBとした場合を表している。次の(1),(2)に答えよ。

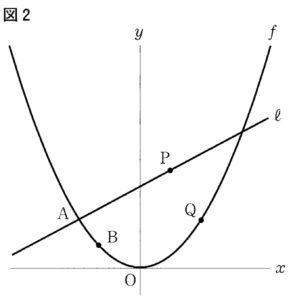
(1) 点Qのx座標を3, 2点P,Qを通る直線とy軸との交点をRとし，点Aと点B,点Aと点R,点Bと点Qをそれぞれ結んだ場合を考える。AB//PQのとき，四角形ABQPの面積と△APRの面積の比を最も簡単な整数の比で表せ。

(2) 下の図3は，図2において，点Pと点Qのx座標が等しく，5より大きい場合を表している。2点B,Qを結んだ直線と直線 $l$ との交点をSとした場合を考える。BS : SQ = 7: 9であるとき，点Pのx座標を下の点線で囲まれた部分の中のように求めた。(あ), (え)に当てはまる数，(い), (う), (お)に当てはまる式をそれぞれ求め, (か)には答えを求める過程が分かるように，途中の式や計算などの続きを書き，答えを完成させよ。

問1

Qの座標とPの座標が分かればPQの長さとPQから点Aまでの距離が分かるので、三角形の面積を出すことができます。

点Qはx=-1を $y=\frac{1}{4}x^2$ に代入してQ(-1, $\frac{1}{4}$ )と分かりますが、点Pを出すにはまず直線 $l$ の式を出さなければいけません。

しかし、二次関数と直線の交点のｘ座標が2つ与えられているという問題設定からして、このポイントより直線の式が出せるのは明らかです(ちなみに、このことは問題を読んだ瞬間に気づいていなければいけませんよ)。よって $l$ の直線の式は $y=\frac{1}{2}x+\frac{15}{4}$ となります。

これにx=-1を代入すれば点Pの座標が出て、P(-1, $\frac{13}{4}$ )です。従って△PAQは以下のように高さ2，底辺の長さが3の三角形になります。

Rendered by QuickLaTeX.com

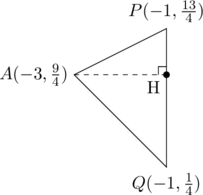
従って、答えは△APQ＝3 $cm^2$ です。

問2

（1）

今回求めたいのは、四角形ABQPの面積と△APRの面積の比です。まずはどうやったらこれが求められるのか？というのを考えておきましょう。

まず、AB//PQという条件が与えられていますね。よって四角形ABQPというのが実は台形であることが分かります。ここで、面積比は共通部分以外に注目することを思い出しましょう。この台形ABQPと△APRは高さが同じですね。それぞれの面積公式を見てみれば、

台形の面積＝ $\frac{1}{2}$ ×(上底＋下底)×高さ
三角形の面積＝ $\frac{1}{2}$ ×底辺×高さ

です。このうち” $\frac{1}{2}$ ×高さ”が今回は同じ値となりますから、結局面積比は共通しているもの以外で決まり

台形ABQP：△APR＝(上底AB＋下底PQ)：底辺PR

ということになります。

ここまでの考察をもとに三平方を使ってAB,PQ,PRを求める、という方針でも良いですが、今回問われているのは比であることに気をつけるともう少し計算を楽にすることができます。

比は軸に飛ばせ、というポイントを思い出しましょう。今回はAB//PQですから、AB：PQ：PRは結局これらの線分をｘ軸に飛ばしたものの長さの比、つまり

AB:PQ:PR＝(点Aと点Bのx座標の差):(点Pと点Qのx座標の差):(点Pと点Rのx座標の差)

です。ここまで来れば、結局答えを出すために必要なのは点A,B,P,Q,Rのx座標であると言うことが分かりますね。では実際に計算して求めてみましょう。

点A,B,Q,Rのx座標は問題文からすぐ分かりますが、点Pだけ少し計算する必要があります。問題文よりA(-3, $\frac{9}{4}$ ), B(-2,1), Q(3, $\frac{9}{4}$ )です。直線PQはABに並行で点Qを通る直線ですから、定点公式より $y=-\frac{5}{4}x+6$ ですね。直線PQと直線 $l$ 、つまり $y=\frac{1}{2}x+\frac{15}{4}$ の交点が点Pですから、計算するとPのx座標は $\frac{9}{7}$ となります。

よって、ｘ座標の差で考えると、

AB:PQ:PR＝1: $\frac{12}{7}$ : $\frac{9}{7}$ =7:12:9

となり、結局

台形ABQP:△APR＝AB＋PQ:PR=7+12:9=19:9

が答えとなります。

（2）

答えに誘導がバッチリついているので、これは乗っかれば良いだけですね。

(あ)は、先ほど求めた直線 $l$ の式 $y=\frac{1}{2}x+\frac{15}{4}$ にx=-2を代入して、 $\frac{11}{4}$ です。

(い)も同じく直線 $l$ に代入するだけで、 $\frac{1}{2}t+\frac{15}{4}$ です。

(う)は放物線ｆに代入するので、 $\frac{1}{4}t^2$ ですね。

(え)はCBの長さです。大きい方(点Cのy座標)から小さい方(点Bのy座標)を引けば良いので、 $\frac{11}{4}$ -1= $\frac{7}{4}cm^2$ となります。

(お)も同様に点Qのy座標から点Pのy座標を引いて、 $\frac{1}{4}t^2-\frac{1}{2}t-\frac{15}{4} cm^2$ です。

(か)ではCB:PQ=7:9に、(え)、(お)で求めたものを代入すれば良いだけです。つまり、

\frac{7}{4}:\left(\frac{1}{4}t^2-\frac{1}{2}t-\frac{15}{4}\right)=7:9\\ \therefore \ t^2-2t-24=0\\ \therefore \ t=6,-4

ただし、t>5という条件がもともとあったので、それを満たすのはt=6であることに注意しましょう。

よって点Pのｘ座標は6となります。