等積変形は、三角形の面積がらみの発展問題で非常によく出てくる考え方です。
これを使うことで、「面積の等しい三角形」というキーワードに賢く対処することができます。
今回は、そんな基本的な等積変形の考え方・およびその発展形を扱っていくとしましょう。
今回のポイントはこちら。
一辺を共有する面積の等しい三角形は、等積変形を使え!
基本編…「面積が等しい」パターン
まずは座標なしで
そもそも三角形の面積とは、底辺の長さと高ささえ決まってしまえば確定するものです。
(三角形の面積)=\frac{1}{2}\times(底辺の長さ)\times(高さ)つまり、底辺の長さも高さも等しい二つの三角形は、面積が等しいわけです。
では質問です。
底辺の長さと面積が等しい二つの三角形は、高さが等しいですか??
…答えはイエスですね。
だったら、底辺からの高さが等しい点を結ぶと、それは底辺と平行な直線になるはずです(平行な線同士の距離はどこをとっても等しいから)。
つまり、下図で\triangle{ABC}と\triangle{ABD}の面積が等しいとすると、AB//CDなわけです。
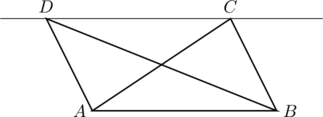
さらに言えば、
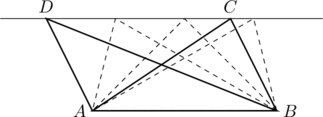
のように頂点をうつしたどの点線三角形も、同じ面積になりますね。
以上のように、底辺の平行線上なら、頂点をうつしても面積は変わらない。
これが等積変形の基本的な考え方です。
座標上で等積変形
さて本題の、座標上での等積変形に移ります。
よくあるシチュエーションは、以下の例のように「二次関数・三角形・面積等しい」というキーワードがそろっているやつですね。
以下の図において、二次関数上にあって\triangle{OAB}=\triangle{OAC}となるような点Cを求めよ。(点Bと点Cは一致しない。)
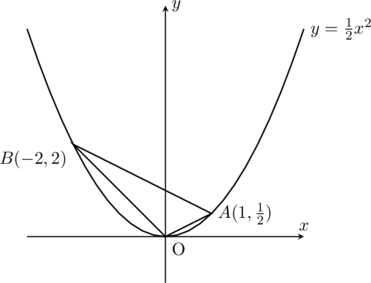
さて、先ほどまでの話を踏まえると\triangle{OAB}と\triangle{OAC}について、
- OAを共有しているので、ここを底辺とみれば良い。
- \triangle{OAB}=\triangle{OAC}ゆえ、OAと平行で点Bを通る直線上に点Cはある。
- 問題文より、点Cは図中の二次関数上にあるという設定。
- 点Cは2.の直線上かつ3.の二次関数上にあるので、これらの交点である。
というふうに考えられます。
2.まで等積変形の考え方を使い、4.で二次関数上にあるという設定と組み合わせる感じです。
では計算しましょう。
OAの傾きが\frac{1}{2}なので、OAと平行で点Bを通る直線は定点公式よりy=\frac{1}{2}x+3。よってy=\frac{1}{2}x^2と連立して:
\begin{aligned}
\frac{1}{2}x^2&=\frac{1}{2}x+3\\
\therefore\ &\frac{1}{2}x^2-\frac{1}{2}x-3=0\\
\therefore\ &x^2-x-6=0\\
\therefore\ &(x-3)(x+2)=0\\
\therefore\ &x=-2,\ 3
\end{aligned}を得ます。ただしx=-2だと点BとCが一致してしまうのでダメですね。
よってx=3であり、答えはC(3, \frac{9}{2})となります。
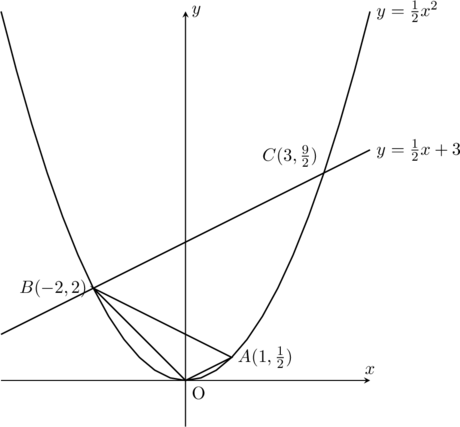
以上が、座標上での等積変形の典型例です。
数値が変わっても上のように考えることには変わりはありません。
このやり方、本当に頻出なので絶対マスターしてくださいね。
というわけで今回のポイントです。
一辺を共有する面積の等しい三角形は、等積変形を使え!
応用編…「面積が2倍」パターン
上の等積変形の考え方を応用すると、ちょっと変わった問題も似たように解くことができます。
どんな問題かというと、ある三角形と一辺を共有していて、面積はそのn倍であるような三角形を求めよ、みたいなやつです。
例題で見ていきましょう。
以下の図において、二次関数上にあって\triangle{OAB}=2\triangle{OAC}となるような点Cを2つ求めよ。

という例題を考えていきましょう。
黄色い下線部以外は、さっきまでの例題と同じ設定になっています。
今回は底辺共有で面積が二倍の三角形を作るという設定です。
だったらもちろん高さ二倍の点を作ろうという発想になりますね。
さきほど求めたy=\frac{1}{2}x+3は、\triangle{OAB}と同じ高さの点の集まりです。だからイメージとしては、
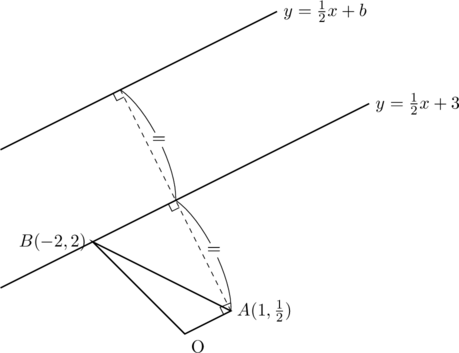
となるようなy=\frac{1}{2}x+bの、切片bがほしいわけですね。
ここで、この図にy軸をつけて、平行なことを利用して少し点線をずらすと…

合同な△OXYと△SZYが見えて、OY=SYであると分かります。
これもある意味、XY:YZ=1:1という比を軸に飛ばしているのですね。(何を言っているのか分からない人はリンク先を復習しましょう。)
よってOY=YS=3ですから、S(0,6)と分かり、b=6を得ます。
あとはy=\frac{1}{2}x+6とy=\frac{1}{2}x^2の交点を求め、さっきの例題と同じように解けば、求める点はC(-3,\frac{9}{2})またはC(4,8)となります。
この例題を応用すれば、一辺さえ共有している3倍や4倍の三角形も作ることができます。
また今回、比を軸に飛ばすというポイントがまた出てきました。
解説記事の相似(合同)のやり方とは少し変えたやり方をしているので、どこが違うのか確認しておきましょう。
今回の宿題
- 中学3年の単元「二次関数」などから、三角形の問題10問以上
を、今回の説明を意識して解いてみてください。
学校で配られた問題集でも、ネット上の問題でも大丈夫です。


