2020年度都立立川高校の入試で出題された数学の解説をします。今回は大問3,4の解説です。
大問1,2はこちら。
大問3は、問1がとても良い問題だったと思います。浅く言えば「気づけば一発」というタイプの問題なのですが、どのように気づくのか?というところを突き詰めると良い勉強になりますね。証明はそのぶん簡単に設定されていたので、そういう意味でもバランスがとれた大問でした。
大問4は考えさせる問題でした。まあそもそも整数問題は考えることが多いのですが、多くの受験生はなんとなく解き進めてなんとなく正解してしまいがちです。そうなると安定して問題を解く訓練になりませんから、いろいろな角度からきちんと考える訓練をしましょう。
今回初出のポイントはこちらです。
1つに定まるものを求める時は、「どんな条件によって1つに定まっているのか」に注意せよ!
大問3
下の図 1 で,△ ABC は AB = 2 cm で,3 つの頂点が全て同じ円周上にある正三角形である。次の各問に答えよ。

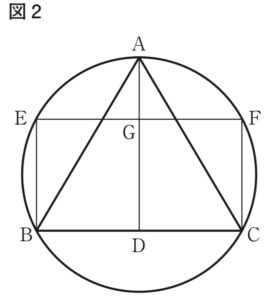
〔問 1〕 下の図 2 は,図 1 において,頂点 A から辺 BC に引いた垂線と辺 BC との交点を D とし,頂点 B,頂点 C からそれぞれ線分 AD に平行に引いた直線と円との交点のうち,頂点 B,頂点 C と異なる点をそれぞれ E,F とし,点 E と点 F を結んだ線分 EF と線分 AD との交点を G とした場合を表している。AD =√3 cm のとき,線分 AG の長さは何 cm か。
〔問 2〕 下の図 3 は,図 1 において,頂点 B を含まない AC 上にあり,頂点 A,頂点 C
のいずれにも一致しない点を H とし,頂点 C と点 H を結んだ線分 CH を H の方向に延ばした直線上にある点を I とし,円の外部にあり,CI = CJ = IJ となるような点を J とし,頂点 A と点 J を結んだ線分 AJ と,頂点 B と点 I を結んだ線分 BI との交点を K とし,頂点 B と点 H,頂点 C と点 J,点 I と点 J をそれぞれ結んだ場合を表している。ただし,線分 CI の長さは辺 CA の長さより短いものとする。次の⑴,⑵に答えよ。
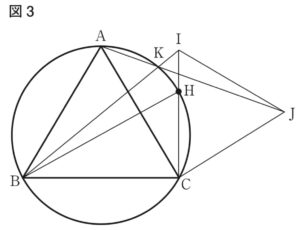
⑴ △ ACJ ≡△ BCI であることを示し,4 点 A,B,C,K は 1 つの円周上にあることを証明せよ。
⑵ ∠ABK = 18°,∠HBC = 28°であるとき,∠AJI の大きさは何度か。
問1
今回問われているのはAGの長さですから、これをxと置きます。
さて問題の図形をぱっと見て、すぐに分かる反応するべき形は
のあたりですね。未知数1つより、式を1つ立てたいですから、例えば相似な図形の辺をxで表していけばいいんじゃないかなぁと考えます。特別角の三角形の辺の比より、BD=1=EGですから、EH+HG=1とできますから、蝶々型の相似の上でEHとHGをxで表そうとしてみますが…
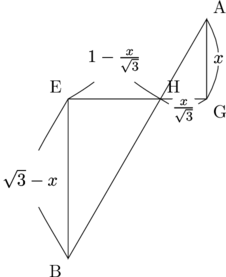
EH=1-\frac{x}{\sqrt{3}}、HG=\frac{x}{\sqrt{3}}ですから、EH+HG=1という式は結局1=1となってしまい、これではxは求められません。
蝶々型ではなく角共有型を使ったとしても同じようなことになります。なぜこのようなことになるのか?それは、このような考え方では円の情報を使えていないからです。以下の図を見てみましょう。
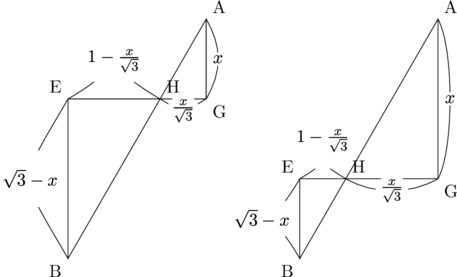
線分EGが左図のように上の方にあっても、右図のように下の方にあっても、xで示される辺の長さは変わりませんね。こうやってEGを上下させたときちょうど外接円上に点Eがくる、というのが今回の問題設定なので、それを使わずにxの値が1つに定まるわけがありません。
このように、問題文から情報を抽出するとき意図せず必要な情報を無くしてしまうことは割とよくあります。線分の長さや点の位置など、1つに定まるものを求める際はどんな条件によって1つに定まっているのかを考えると見通しが良いことが多いので、気にしてみてください。
1つに定まるものを求める時は、「どんな条件によって1つに定まっているのか」に注意せよ!
というわけで、円の情報を使うことを意識して問題を解いていきましょう。
ポイントを意識しつつ解くやり方としては、直径の円周角に反応するというものがあります。例えば、今回∠BEFが直角です。円周上に直角…と言えば、直径の円周角は90°、というポイントがありましたね。よって線分BFが円の直径で、BFとADの交点が円の中心Oになります。三角形EBFが特別角の三角形であることに気づけば、外接円の半径などを考えればBEの長さが分かり、よってAGの長さも出せます。
また簡単なのは、三角形AEGが特別角の三角形であることに気づくことでしょう。∠FCA=30°であり、よって円周角の定理から∠AEFも30°です。△AEBの内角の和を考えれば∠EAB=30°ですから、結局△AEGは1:2:√3の三角形と分かりますね。あとは先に述べたとおりEG=1であることを使えば、AG=\frac{\sqrt{3}}{3}が答えです。
問2
(1)
図形の合同や相似の証明では、証明すべき結論から逆算して考えていくことが大切です。
たとえば今回だと、△ACJ ≡△BCIです。合同なら対応する辺・角の大きさは等しいはずですから、それぞれの要素について、その理由を考えてみると…
- 正三角形の辺なので、BC=AC、IC=JC
- 正三角形の内角60°と∠ACIの和で表せるので、∠ACJ=∠BCI
と分かります。これより二組の辺とその間の角がそれぞれ等しいので、合同が言えますね。
点が同一円周上にあるときに使うのは、99%円周角の定理の逆です。
今回点A,B,C,Kの並びでは等角型が使えそうです。直前に証明した△ACJ ≡△BCIを踏まえれば、対応する∠JAC=∠IBCより、円周角の定理の逆から点A,B,C,Kは同一円周上にあると言えます。
△ACJ ≡△BCIの証明という誘導にきちんと乗っかれるようにしましょう。何も考えずに∠BAC=∠BKCを示そうなどと考えると沼にはまってしまいます。
(2)
∠ABK = 18°,∠HBC = 28°という設定は数字が中途半端ですから、特別角とかを積極的に活用する感じではなさそうです。
地道に角を図に書き込んでいく系の問題かなぁ…とあたりを付けつつ、求めるもの∠AJIを見てみましょう。するとこれは、先ほど合同を証明した△ACJの内角∠AJCと合わせて60°(=∠CJI)になっていますね。だから∠AJCの大きさが分かれば、∠AJIの大きさが分かると言えます。
先ほど合同を示しているので、∠AJC=∠BICです。∠BICって、円周角でもないし正三角形の内角でもない微妙なところにありますから、これを直接求めるのは難しそうです…よって他の2つの内角∠IBCと∠BCIに目を向けてみます。すると、
- ∠IBC=∠ABC – ∠ABK=60° – 18°=42°
- ∠BCI=∠ACH+∠BCA=∠ABH+60°=(∠ABC – ∠HBC)+60°=60° – 28°+60°=92°
ということが正三角形の内角の和と、円周角の定理より分かりますね。
あとは今までの考えを逆にたどって、
- ∠BIC=180° – (∠IBC+∠BCI)=46°
- ∠AJC=∠BIC=46°
- ∠AJI=60° – ∠AJC=14°
となって、答えは14°であると分かります。このように、欲しいものから逆算して考えていくと結局最短ルートを進めることが多いです。
大問4
下の図 1 で,四角形 ABCD は AB = 104 cm,AD = 156 cm の長方形である。四角形 ABCD の内部に,辺 AD に平行で辺 AD と長さが等しい線分を,となり合う辺と線分,となり合う線分と線分のそれぞれの間隔が 8 cm になるように 12 本引き,辺 AB に平行で辺 AB と長さが等しい線分を,となり合う辺と線分,となり合う線分と線分のそれぞれの間隔が 6 cm になるように 25 本引く。次の各問に答えよ。

〔問 1〕 図 1 において,頂点 A と頂点 C を結んだ場合を考える。線分 AC が,辺 AD に平行な線分または辺 AB に平行な線分と交わるときにできる交点は何個あるか。ただし,辺 AD に平行な線分と辺 AB に平行な線分の交点および頂点 A,頂点 C は除くものとする。
〔問 2〕 下の図 2 は,図 1 において,辺 AD に平行な線分と辺 AB に平行な線分との交点のうちの 1 つを P とし,点 P を通り辺 AD に平行に引いた線分と辺 AB との交点を Q,点 P を通り辺 AB に平行に引いた線分と辺 AD との交点を R とした場合を表している。ただし,点 P は辺 AB 上にも辺 AD 上にもないものとする。四角形 AQPR において,PR = 2 PQ となるもののうち,面積が最大になる場合の面積は何 cm^2 か。

〔問 3〕 底面が縦 6 cm,横 8 cm の長方形で,高さが 9 cm の直方体のブロックを十分な数だけ用意し,⑴,⑵の手順に従って直方体 S,直方体 T を作る場合を考える。
⑴ ブロックの底面を図 1 の直線でできたマスに合わせて置き,ブロック同士の側面がぴったり重なるように隙間なく並べて,底面が四角形 ABCD の内部に収まるような高さが9 cm の直方体 S を作る。
⑵ ⑴で作った直方体 S を何個も作り,直方体 S の高さを変えずに隙間なく 2 段,3 段,4 段,……と何段か縦に積み上げて直方体 T を作る。
この直方体 T が立方体になるとき,使われるブロックは全部で何個か。ただし,答えだけでなく,答えを求める過程が分かるように,途中の式や計算なども書け。
問1
対角線ACと、マス目の掛け線との交点を求める問題です。縦線を12本、横線を25本の計37本を越えて対角線ACは点Aから点Cまで繋がっていますから、点A,Cを除き最大で37個の交点があります。
しかし今回の問題設定では、縦線と横線の交点を対角線ACが通るとき、つまり対角線ACが縦線と横線を同時に横切るときは、交点をカウントしません。よって、このカウントされない交点の数を数え、それを2倍したもの(縦線と横線の2回ぶんということ)を37個から引いたものが答えです。
カウントされない交点とはどんな点かを考えましょう。点Aと点Cはまさに、対角線ACが縦線と横線を同時に横切る典型的な点ですね。そしてこの2点は、線分ACを対角線とする長方形の頂点です。つまり、カウントされない交点とは、線分ACを対角線とする長方形の頂点ではないか?と考えられます。そして線分ACを対角線とする長方形とは、以下のように長方形ABCDと相似な長方形です。
従って、そのような長方形で最小のものを探すと、

長方形ABCDの縦横比104:156=2:3より、横1マス×縦2マスで同じ比率8:12=2:3の長方形が見つかります。この長方形を13個斜めに並べると、直線ACになりますから、点Aと点Cを除くことに注意すると、点Aと点C以外にカウントされない交点は12個です。
よって答えは37 – 12×2=13個です。
…と、ここまで解説しましたが実際の試験では図が与えられているので、その図に対角線を書き込んで数えた方が早い気がします。どう解くかは皆さんのお好みで構いません。
図1を見たとき、「あ、xy座標っぽいな」と思った人も多いのではないでしょうか。xy座標として解くなら、この問1は格子点の問題にほかなりませんね。
ただし今回は1マスの縦と横の長さが違うので、そのままではxy座標として解くことはできません。ただし逆に言えば、縦と横の長さをそろえればxy座標として解くことができます。
例えば、横の長さを4分の3倍してみましょう。すると1マスは6×6cmとなり、ABの長さは78cmとなります。するとまさに、正方形がならんだxy座標と同じ形になりますね。
変形した長方形ABCDをxy座標とみなせば、座標はA(0,0), B(13,0), C(13,26), D(0,26)と表せ、直線ACはy=2xです。よって直線AC上ではx座標が整数のときy座標も整数になりますから、点Aと点Cを除いた0<x<13の範囲でxが整数となるものの数を数えれば確かに12個となります。
あとは上と同じように考えて、37 – 12×2=13個が答えです。
問2
今回長方形PQRSの形は1つには定まっていませんね。限られた範囲の中でPQRSの形が変化するので、その中で最大面積のものを答えよ…という問題なわけですが、「範囲の中の最大値を求める」って響きで思い浮かぶものはありませんか?
…そうです、変域の中でグラフの最大値を求める問題ですね。よって今回は、縦とか横の長さを文字で表して面積のグラフを書けば良いのでは?と発想できます。
とりあえず、分からないものは文字で置け!というポイントがありますから、分からないものを文字で置いてみましょう。
まず、求めたい面積をSと置きます。
次に長方形PQRSの縦の長さを6x, 横の長さを8yと置きます。なぜx, yではなく6x, 8yと置くのかと言うと、PR,PQは掛け線の上にあるので、縦の長さは必ず6の倍数に、横の長さは必ず8の倍数になるからです。
言い換えれば、四角形PQRSの縦マスの数をx、横マスの数をyと置いたとも言えますね。よって、x,yは0<x≦26、0<y≦13を満たす整数です。この変域がこの後で効いてきます。
ここまで来ると、問題文の条件PR=2PQを文字を使って表せますね。PQ=6x、PR=8yですから8y=12xです。
以上より、こんな式が立てられます。
\left\{
\begin{aligned}
S&=48xy\\
12x&=8y\\
0 &< x \leqq 26\\
0 &< y \leqq 13\\
\end{aligned}
\right .12x=8yを使って変数を1つ消すことができます。ここでx, yの変域に注意しましょう。よく見るとxの変域よりyの変域の方が厳しいですね。これはどういう意味かというと、上の不等式より
\left\{
\begin{aligned}
0 &< 12x \leqq 288\\
0 &< 8y \leqq 104\\
\end{aligned}
\right .となり、12x=8yは左辺の範囲が右辺の取り得る範囲より狭いということです。したがってyの変域を採用した方が不都合が少ないので、xを消すとしましょう。
さらに言えば、12x=8y、つまり3x=2yの両辺が整数であるというところからyが3の倍数であることにこの時点で気づいておくと良いでしょう。もちろん、x,yが整数であることに注意できていれば後から気づくこともできるはずです。
以上より、式はこのように変えられます。
\left\{
\begin{aligned}
S&=32y^2\\
y&=3\ or\ 6\ or\ 9\ or\ 12\
\end{aligned}
\right .ここまで来れば、グラフを書かずともSが最大値を取るのはy=12の時であるのが一目瞭然です。よって答えは4608cm^2です。
問3
問2を参考にして、x,yの文字をそのまま使います。
また新たに高さの話が出てきたので、何段積むかというのをz段と表しましょう。
立方体は縦・横・高さが等しいですから、以下のような式が立てられます。
\left\{
\begin{aligned}
6x&=8y=9z\\
0 &< x \leqq 26\\
0 &< y \leqq 13\\
0&< z
\end{aligned}
\right .この時点で、x, y, zが全て整数だということを踏まえると、6x=8y=9zがどのような値を取るかが絞られます。6x=8y=9z=Aと置くと、Aは6の倍数であり、8の倍数であり、9の倍数です。つまり6, 8, 9の最小公倍数72の倍数になっているということですね。
ここでyの変域を見れば、A=72しかあり得ません。たとえばAが72×2=144のとき、y=18となって変域に当てはまらなくなってしまいます。
以上より6x=8y=9z=72なので、x=12, y=9, z=8です。
よってブロックの個数は12×9×8=864個です。

