平面図形の問題を解く際、「相似な図形を利用する」ということをしなければいけない場合が結構あります。皆さんも「あ、ここの相似使えば良かったのか!気づかなかった…」という経験があるのではないでしょうか?
相似を利用させられる問題のパターンは大抵2つです。
- 相似な2つの図形が近くにあって、気づきやすい場合
- 相似な2つの図形が遠くにあって、気づきにくい場合
2.の場合が解けなくてがっかりすることが多いですが、実際2.の場合は誘導(証明問題など)がつくことが多いです。よってそんなに心配しなくても良いし、むしろ誘導をきちんと利用すると言うことを意識すべきでしょう。
大事なのは1.の場合です。これは絶対気づかなければいけないし、利用できなければいけません。そんな気づきやすい場合の形ってどんな形?というのをまとめるのが今回です。
相似で大事な3つの型、ばっちりマスターしてください!!今回のポイントはこちらです。
角共有型・蝶々型・反転型の相似に注意せよ!
角共有型
角共有型の相似とは、以下のような場合です。△ABC∽△ADEとなっています。

とっても基本的な図形ですが、探そうという意識が無ければ問題の中で案外気づかないものです。必ず見つけられるように意識しましょう。
中線連結定理
中線連結定理とは、角共有型の特別な場合です。
下図のような角共有型の相似において、点BとCがそれぞれ辺ADとAEの中点ならば、
- △ABC∽△ADE
- BC // DE
が成り立つ。

蝶々型
蝶々型の相似とは、以下のような場合です。△ABC∽△ADEとなっています。

角共有型も蝶々型も平行線が含まれるので、平行四辺形とからめて出題されることが多いです。
平行四辺形に潜む角共有型と蝶々型
以下の例は基本中の基本のやり方を示しています。
以下の平行四辺形ABCDで、点E,Fはそれぞれ辺BC,CDの中点である。BP:PQ:QDの比を最も簡単な整数比で答えよ。

対角線BDを点P,Qで分割した比を出す問題です。話題になってるのは対角線BDなので、BDのあたりをよく見ると…まず△PAD∽△PEBという蝶々型の相似が見えますね。この相似比を見れば、BP:PD=1:2だということが分かります。

さて、ここからが本題ですが…AFとBCを延長するような補助線を引くと、蝶々型の相似が2つ(△QAD∽△QGBと△FCG∽△FDA)が見えます。
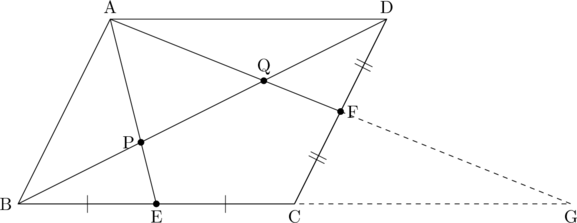
このように、補助線を引いて知っている形を無理矢理作るというやり方はよくやります。だから知っている形・注意すべき形をまとめておくことが大事なのです。
△FCG∽△FDAの相似比を見ればAD=CGと分かり、よって△QAD∽△QGBの相似比は1:2。だからBQ:QD=2:1と分かります。

ここまでで蝶々型の相似を3組使って情報を集めてきて、対角線BDは点P,Qによって以下のように分けられていることが分かりました。
![]()
よってまとめると、BP:PQ:QD=1:1:1です。
反転型
最後に紹介する形は、反転型です。以下の図のような形で、△ABC∽△ADEとなっています。

上2つの形と違い、この形を意識したことのある人は少ないのではないでしょうか。基本問題では確かにあまり出てきませんが…受験問題になると、地味によく出てくる形となっています。
ぱっと見て分かると思いますが、なんか捉えどころの無い、意識しづらい形をしていますよね。だからこそ受験生を引っかけるためによく狙われるのです。狙い通り引っかかるのも悔しいですから、きちんと気づけるように意識しておきましょうね。
では以上3つの形をポイントにして、終わりにするとしましょう。
角共有型・蝶々型・反転型の相似に注意せよ!
今回の宿題
- 中学2年の単元「空間図形」などから、問題15問以上
を、今回の説明を意識して解いてみてください。
学校で配られた問題集でも、ネット上の問題でも大丈夫です。


